固体物性の分野を学ぶと、結晶構造の議論においてどうしても避けられないのが逆格子ベクトルの話題だ。筆者は化学専攻ではないが、電気電子専攻として半導体物性を勉強しており、最初に当たった壁がこれだった。

学部生は初回の授業で1次元での話を出され「ああ周期性あるからフーリエ変換するんでしょ、分かる分かる」と言っていると、多次元化したとたんに『ブラべ格子』『基本並進ベクトル』『逆格子ベクトル』『ブリルアンゾーン』などと矢継ぎ早に分かったような分からないような単語を繰り出されて身悶えすることになる。

この記事では、多次元空間上の周期性のある関数を多次元フーリエ変換すると自然に逆格子ベクトルが発生することを確認したいと思う。

教科書的な逆格子ベクトルの導入

よくある教科書だと以下のような形で逆格子ベクトルを導入する。見飽きた人は読み飛ばしてよい。

周期性のある関数$f$があるとして、それが周期性のために以下のように表せると仮定する。

$$f(\mathbf{x})=\sum C(\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}}$$

周期性 $f(\mathbf{x} + \mathbf{a})=f(\mathbf{x})$ があるので、以下が成り立つはずである。

$$f(\mathbf{x})=\sum C(\mathbf{k}) e^{i \mathbf{k} \cdot (\mathbf{x}+\mathbf{a})}=\sum C(\mathbf{k}) e^{i \mathbf{k} \cdot (\mathbf{x})}$$

$$\sum C(\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} e^{i \mathbf{k} \cdot \mathbf{a}}=\sum C(\mathbf{k}) e^{i \mathbf{k} \cdot (\mathbf{x})}$$

$$\Rightarrow e^{i\mathbf{k}\cdot \mathbf{a}}=1$$

$$\Rightarrow \mathbf{k}\cdot \mathbf{a}=2mi\ (mは整数)$$

だから$\mathbf{k}$は$\mathbf{a}$と直交で、全ての基本並進ベクトルと直交になるように$\mathbf{k}$を決めると何やら逆格子とやらが生まれるらしい。

どこの教科書も大筋はこんなものだろう。狐につままれたような話である。

以下はこのよく分からない説明の行間を自分なりにガチガチに補完した内容である。

フーリエ変換とフーリエ級数展開について

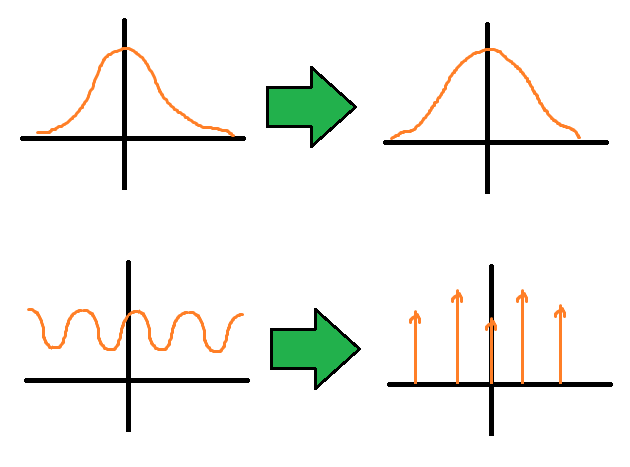
そもそも1次元の場合において、周期性のある関数を"フーリエ変換"すると等間隔の点だけが残り、フーリエ級数展開と一致することを確認したいと思う。

(複素)フーリエ変換の定義式はこうだ。

$$F(\omega)=\int_{-\infty}^\infty f(t) e^{-i\omega t} dt$$

これはフーリエ級数展開ではなくフーリエ変換なので、関数に周期性は有っても無くてもよい。

というか初学者向けには「周期性があると絶対可積分ではなくなるのでフーリエ変換するなフーリエ級数展開しろ」ということになっているが、後述するように$\delta$関数で表現するとどうにかなる。

ここで$f(t)$に周期$T$があり、以下のようにフーリエ級数で表せたとしよう。

$$f(t)=\sum c_n e^{i\frac{2\pi}{T}nt}$$

これをフーリエ変換の式に入れるとこうなる。

$$F(\omega)=\int_{-\infty}^\infty \left(\sum c_n e^{i\frac{2\pi}{T}nt}\right) e^{-i\omega t} dt$$

$$=\int_{-\infty}^\infty \sum c_n e^{i\left(\frac{2\pi}{T}n-\omega\right)t} dt$$

$$= \sum c_n \left(\int_{-\infty}^\infty e^{i\left(\frac{2\pi}{T}n-\omega\right)t} dt\right)$$

$$= \sum c_n \cdot 2\pi \delta\left(\omega-\frac{2\pi}{T}n\right)$$

このように、周期$2\pi / T$の等間隔の点だけ$\delta$関数で尖って残ることが分かった。

周期性のない関数をフーリエ変換すれば連続関数になるし、周期性のある関数をフーリエ変換すれば離散化する(等間隔の点だけが離散的に残る)のである。この対応関係を頭に入れておいて欲しい。

基本格子ベクトル

多次元化を考える準備として基本格子ベクトル(基本並進ベクトル)のことを考えよう。

1次元の周期性とは「数直線上を一定距離進むと同じ値になる」というものだった。

$$f(x + a)=f(x)$$

多次元関数(物理学徒には「場」と呼んだ方が良いかもしれない)における周期性とはどのようなものか？これは「あるベクトルだけ進むと同じ値になる」ものとして考える。

$$f(\mathbf{x}+\mathbf{a}) = f(\mathbf{x})$$

この$\mathbf{a}$を基本格子ベクトルと呼ぶ。

注意しておきたいのは、互いに独立したこのようなベクトルが最大で次元の数だけあるということだ。

$$f(\mathbf{x}+\mathbf{a_1}) = f(\mathbf{x})$$ $$f(\mathbf{x}+\mathbf{a_2}) = f(\mathbf{x})$$ $$\vdots$$

この$n$個のベクトルが張る$n$次元平行体図形(※2次元では平行四辺形、3次元では平行六面体)が$n$次元空間に整然と並んでいるところを考えると、周期性からその内部はどれを見ても全く同じになることが分かる。これを単位格子とか単位胞とか言ったりする。

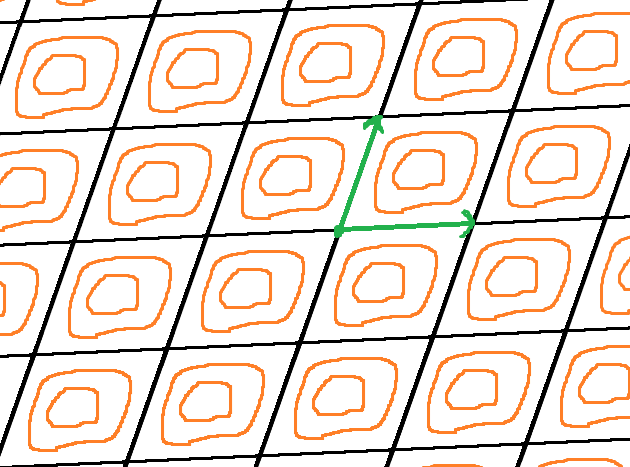
また$n$個の基本格子ベクトルは互いに独立なベクトルなのであるから、線形空間の基底にもなれる。任意の空間座標は基本格子ベクトルの線型結合として表せる。

$$\mathbf{x}=u_1\mathbf{a_1}+u_2\mathbf{a_2}+\ldots=\sum u_j \mathbf{a_j}$$

多次元フーリエ変換

ようやく本題に入る。

通常の1次元のフーリエ変換は以下のような数式だった。

$$F(\omega)=\int_{-\infty}^\infty f(t) e^{-i\omega t} dt$$

フーリエ変換は1次元関数$f(t)$から1次元関数$F(\omega)$に写す変換である。

そして、多次元フーリエ変換は以下のように定義される。

$$F(\mathbf{k})=\idotsint f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} d\mathbf{x}$$

$\mathbf{k}$も$\mathbf{x}$もベクトルなので$e$の肩が内積になっているところだけ違っていて、他は1次元と変わらない。

あとは$n$次元なので$n$重積分になっている。より具体的に書き下せば以下のようになる。

$$=\idotsint f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} dx_1 dx_2 \ldots dx_n$$ $$=\int_{-\infty}^\infty dx_1 \int_{-\infty}^\infty dx_2 \ldots \int_{-\infty}^\infty dx_n f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}}$$

ここを確認しておこう。

$n$次元フーリエ変換は$n$次元空間上の関数$f(\mathbf{x})$から$n$次元空間上の関数$F(\mathbf{k})$に写す変換である。

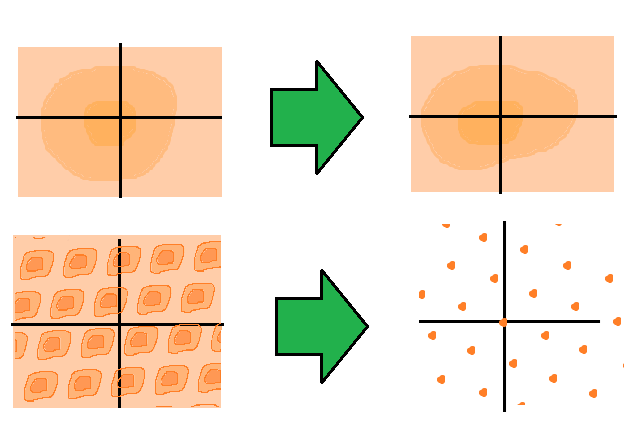
通常の1次元フーリエ変換では、周期性のある関数をフーリエ変換すると離散化するのだった。これは多次元でも一般化出来て、周期性の無い多次元関数を多次元フーリエ変換すれば連続な多次元関数になるが、周期性のある多次元関数を多次元フーリエ変換すれば格子点だけが残る、というのがこの記事の本題である。

計算

$n$次元空間上の関数$f(\mathbf{x})$に基本格子ベクトル$a_1, a_2, \ldots a_n$で表される周期性があるとしよう。これを多次元フーリエ変換する。

$$F(\mathbf{k})=\idotsint f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} d\mathbf{x}$$

まずはこれを扱いやすくしたい。

さしあたりこの式だと直交座標系 $x_1, \ldots, x_n$ での積分になっているので、基本格子ベクトルを基底とする座標系$u_1, \ldots, u_n$での積分になるよう積分変数変換を行う。

ステップ1. 変数変換

$$\begin{eqnarray}\mathbf{x}&=&x_1 \mathbf{\hat{x}_1} + x_2 \mathbf{\hat{x}_2} + \ldots\\ &=& u_1 \mathbf{a_1} + u_2 \mathbf{a_2} + \ldots\end{eqnarray}$$

$$x_j=u_1 \left(\mathbf{a_1 \cdot \hat{x}_j}\right) + u_2 \left(\mathbf{a_2 \cdot \hat{x}_j}\right) + \ldots$$

細かい計算は省く。斜向座標系なので、球座標などとの変換と違いヤコビアンは定数になる。積分の外に出せてしまうから難しいことは何もない。

$$F(\mathbf{k})=\idotsint f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} dx_1 dx_2 \ldots dx_n$$

$$=|\det \mathbf{J}|\idotsint f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} du_1 du_2 \ldots du_n$$

$$=|\det \mathbf{J}|\int du_1 \int du_2 \ldots \int du_n f(\mathbf{x}) e^{-i \mathbf{k}\cdot \mathbf{x}} $$

関数$f$は $u_1, u_2, \ldots, u_n$ の関数になるので、$f(u_1, u_2, \ldots, u_n)$と書ける。

また、$\mathbf{x}=u_1 \mathbf{a_1} + u_2 \mathbf{a_2} + \ldots$ を用いると以下のように書ける。

$$\int du_1 \int du_2 \ldots \int du_n f(\mathbf{x}) e^{-i \mathbf{k}\cdot (u_1 \mathbf{a_1} + u_2 \mathbf{a_2} + \ldots)} $$

$$=\int du_1 \int du_2 \ldots \int du_n f(u_1, u_2, \ldots, u_n) \left( \prod_{1\leq j \leq n} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right)$$

以下、ヤコビアン$|\det \mathbf{J}|$は定数倍の違いしかないので表記を省略する。

ステップ2. $u_n$に依存する部分を取り出す

ここで関数$f(u_1, u_2, \ldots, u_n)$は、$u_1, u_2, \ldots, u_{n-1}$を固定すれば$u_n$の関数とみなすことが出来る。これを分かりやすくするため関数$f$を以下のように書く。

$$f_{u_1, u_2, \ldots, u_{n-1}}(u_n)$$

これを用いると

$$\int du_1 \int du_2 \ldots \int du_n f_{u_1, u_2, \ldots, u_{n-1}}(u_n) \left( \prod_{1\leq j \leq n} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) $$

$$=\int du_1 \int du_2 \ldots \int du_{n-1} \left( \prod_{1\leq j \leq n - 1} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) \left( \int du_n f_{u_1, u_2, \ldots, u_{n-1}}(u_n) e^{-i u_n \mathbf{k}\cdot \mathbf{a_n}} \right)$$

このように$u_n$に依存する部分を括りだすことが出来る。

もちろん$u_1, \ldots, u_n$は等価なので、$u_n$から始めることに必然性はない。$u_1$からでも良い。

ステップ3. 通常のフーリエ変換を行う

この一番右側の

$$\int du_n f_{u_1, u_2, \ldots, u_{n-1}}(u_n) e^{-i u_n \mathbf{k}\cdot \mathbf{a_n}}$$

の部分は、変数$u_n$に対する通常のフーリエ変換とみなせる。1次元のフーリエ変換のときと同様の議論をしてみよう。

関数$f$は基本格子ベクトル$\mathbf{a_n}$の周期性があるのだからフーリエ級数展開が出来るはずだ。変数変換を行っているので、$u_j$を $+1$ 動かせば、座標$\mathbf{x}$は $+\mathbf{a_j}$ だけ動く。

整数$m$を添え字とする周期$1$のフーリエ級数展開をする。

$$f_{u_1, u_2, \ldots, u_{n-1}}(u_n)=\sum_{-\infty < m < \infty} c_{m}(u_1, u_2, \ldots, u_{n-1}) e^{i 2 \pi m u_n}$$

$c_{m}$はフーリエ係数である。これは $u_1,u_2, \ldots, u_{n-1}$ に依存するのでその関数とした。

これを使うと、

$$\int du_n f_{u_1, u_2, \ldots, u_{n-1}}(u_n) e^{-i u_n \mathbf{k}\cdot \mathbf{a_n}}$$

$$=\int du_n \left( \sum_{m} c_{m}(u_1, u_2, \ldots, u_{n-1}) e^{i 2 \pi m u_n} \right) e^{-i u_n \mathbf{k}\cdot \mathbf{a_n}} $$

$$=\sum_{m} c_{m}(u_1, u_2, \ldots, u_{n-1}) \int du_n e^{i \left(2 \pi m -\mathbf{k}\cdot \mathbf{a_n} \right) u_n}$$

$$=\sum_{m} c_{m}(u_1, u_2, \ldots, u_{n-1}) \cdot 2\pi \delta(2 \pi m -\mathbf{k}\cdot \mathbf{a_n})$$

このようにやはり$\delta$関数が出てきた。ある整数$m$が存在して

$$2 \pi m =\mathbf{k}\cdot \mathbf{a_n}$$

が成り立つときのみ非0になる。

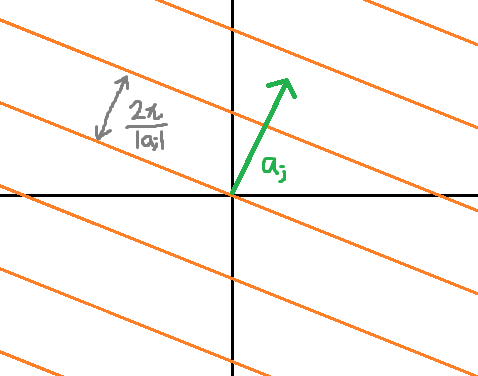
式だけ見ても分かりづらいので$\mathbf{k}$空間でプロットすると、これはベクトル$\mathbf{a_n}$と直交する面で値が非0になり、そのような面が長さ$2\pi/|\mathbf{a_n}|$の等間隔で存在するという形になる。

ステップ4. $u_1$ ～ $u_{n-1}$について同様に行う

先ほどの結果を元の多次元フーリエ変換の式に代入する。

$$\begin{eqnarray} &\int du_1 \int du_2 \ldots \int du_{n-1} \left( \prod_{1\leq j \leq n - 1} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) \\ &\cdot \sum_{m} c_{m}(u_1, u_2, \ldots, u_{n-1}) \cdot 2\pi \delta(2 \pi m -\mathbf{k}\cdot \mathbf{a_n}) \\\\ =&2\pi \sum_{m} \delta(2 \pi m -\mathbf{k}\cdot \mathbf{a_n}) \\ &\cdot \int du_1 \int du_2 \ldots \int du_{n-1} c_{m}(u_1, u_2, \ldots, u_{n-1}) \left( \prod_{1\leq j \leq n - 1} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) \end{eqnarray}$$

式の形を観察すると、積分の中身は$n$が1つ減ってまた同じ形になっていることが分かる。これを利用すれば再帰的に処理していくことができる。

$$\begin{eqnarray} &2\pi &\sum_{m} \delta(2 \pi m -\mathbf{k}\cdot \mathbf{a_n}) & \\ &&\cdot \int du_1 \int du_2 \ldots \int du_{n-1} c_{m}(u_1, u_2, \ldots, u_{n-1}) \left( \prod_{1\leq j \leq n - 1} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) & \\ \\ =&(2\pi)^2&\sum_{m_{n-1}} \delta(2 \pi m_{n-1} -\mathbf{k}\cdot \mathbf{a_{n-1}}) & \\ &&\sum_{m_n} \delta(2 \pi m_n -\mathbf{k}\cdot \mathbf{a_n}) & \\ &&\cdot \int du_1 \int du_2 \ldots \int du_{n-2} c_{m_{n-1}, m_n}(u_1, u_2, \ldots, u_{n-2}) \left( \prod_{1\leq j \leq n - 2} e^{-i u_j \mathbf{k}\cdot \mathbf{a_j}} \right) & \\ \\ =&(2\pi)^n&\sum_{m_1} \delta(2 \pi m_1 -\mathbf{k}\cdot \mathbf{a_1}) & \\ &&\sum_{m_2} \delta(2 \pi m_2 -\mathbf{k}\cdot \mathbf{a_2}) & \\ &&\vdots & \\ &&\sum_{m_n} \delta(2 \pi m_n -\mathbf{k}\cdot \mathbf{a_n}) & \\ &&\cdot c_{m_1, m_2, \ldots, m_n} & \\\\ =&(2\pi)^n&\sum_{m_1, m_2, \ldots, m_n} c_{m_1, m_2, \ldots, m_n}\prod_{1\leq j \leq n} \delta(2 \pi m_j -\mathbf{k}\cdot \mathbf{a_j}) & \end{eqnarray}$$

以上のようにして、$n$個の$\delta$関数の積が出てくることが分かった。

逆格子ベクトルの存在

説明したように、$\delta$関数の成分1つは以下のように基本格子ベクトル$\mathbf{a_j}$に直交する面を作る。

これが $\mathbf{a_1}, \ldots, \mathbf{a_n}$ の$n$個分掛け合わされていて、基本格子ベクトルはどの2つも平行ではないのだから、格子点だけが非0で残ることが分かる。

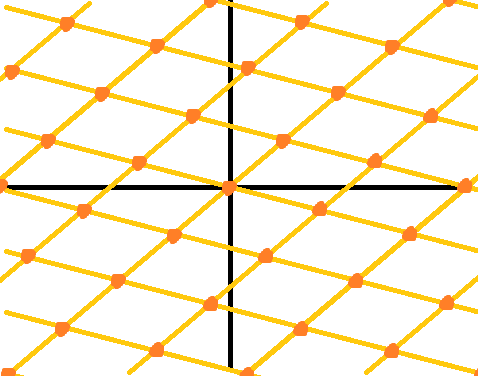
2次元を例に取れば、線と線の交わりは点である。3次元を例に取れば、まず面と面の交わりは線であり、面と線の交わりは点である。このように任意の$n$次元空間について、互いに平行でない$n-1$次元面を$n$個重ねればその交わりは点になる。

これで1次元フーリエ変換の場合と同じように、周期関数の多次元フーリエ変換では格子点だけが成分を持つことが分かった。

格子状に並んでいればそれを表せるベクトルの存在も自明で、これがいわゆる逆格子ベクトルである。

話はここで終わりでも良いのだが、一応実際の値も考えてみよう。

逆格子ベクトルの値

整数$m_1, m_2, \ldots$が存在し、全ての $1\leq j \leq n$ について $2\pi m_j = \mathbf{a_j}\cdot \mathbf{k}$ を満たせばよいはずだ。行列で表すと分かりやすい。

$$\left(\begin{array}{c}2\pi m_1 \\ 2\pi m_2 \\ \vdots \\ 2\pi m_n\end{array}\right)= \left(\begin{array}{c}\mathbf{a_1} \\ \mathbf{a_2} \\ \vdots \\ \mathbf{a_n}\end{array}\right) \mathbf{k}$$

$$\mathbf{k}=\left(\begin{array}{c}\mathbf{a_1} \\ \mathbf{a_2} \\ \vdots \\ \mathbf{a_n}\end{array}\right)^{-1} \left(\begin{array}{c}2\pi m_1 \\ 2\pi m_2 \\ \vdots \\ 2\pi m_n\end{array}\right)$$ $$=2\pi \left(\begin{array}{c}\mathbf{a_1} \\ \mathbf{a_2} \\ \vdots \\ \mathbf{a_n}\end{array}\right)^{-1} \left(\begin{array}{c}m_1 \\ m_2 \\ \vdots \\ m_n\end{array}\right)$$

$\mathbf{a_j}$は$n$次元横ベクトルということにした。$n$個縦に並べれば正方行列になる。

ここで行列$A$を

$$A=\left(\begin{array}{c}\mathbf{a_1} \\ \mathbf{a_2} \\ \vdots \\ \mathbf{a_n}\end{array}\right)$$

とすれば、以下のように表せる。

$$\mathbf{k}=2\pi A^{-1}\left(\begin{array}{c}m_1 \\ m_2 \\ \vdots \\ m_n\end{array}\right)$$

これで逆空間において任意の整数の組$m$に対応した成分が存在することが分かった。

ところでこの式はさらに、

$$\begin{eqnarray} \mathbf{k} &=& 2\pi A^{-1}\left(\begin{array}{c}m_1 \\ m_2 \\ \vdots \\ m_n\end{array}\right) \\ \\ &=& 2\pi A^{-1}\left( m_1 \left(\begin{array}{c}1 \\ 0 \\ \vdots \\ 0\end{array}\right) + m_2 \left(\begin{array}{c}0 \\ 1 \\ \vdots \\ 0\end{array}\right) + \ldots + m_n \left(\begin{array}{c}0 \\ 0 \\ \vdots \\ 1\end{array}\right) \right) \\ \\ &=& 2\pi A^{-1}\left( m_1 \mathbf{e_1} + m_2 \mathbf{e_2} + \ldots + m_n \mathbf{e_n} \right) \\ \\ &=& m_1 (2\pi A^{-1} \mathbf{e_1}) + m_2 (2\pi A^{-1} \mathbf{e_2}) + \ldots + m_n(2\pi A^{-1} \mathbf{e_n} ) \end{eqnarray}$$

という風に書ける。

この $2\pi A^{-1}\mathbf{e_1}, 2\pi A^{-1}\mathbf{e_2}, \ldots$ というベクトル組こそが、いわゆる基本逆格子ベクトルと同じものである。

試しに3次元空間で確かめてみよう。

3次元空間の基本逆格子ベクトル

行列$A$を以下とする。

$$A=\left(\begin{array}{c}\mathbf{a_1} \\ \mathbf{a_2} \\ \mathbf{a_3} \end{array}\right) =\left( \begin{array}{ccc} a_{1x} & a_{1y} & a_{1z}\\ a_{2x} & a_{2y} & a_{2z}\\ a_{3x} & a_{3y} & a_{3z}\end{array}\right)$$

逆行列の導出はネット上にいくらでも転がっているので割愛する。

$$A^{-1}=\frac{\tilde{A}}{|A|}$$

$$=\frac{1}{a_1\cdot(a_2\times a_3)} \left(\begin{array}{ccc} a_{2y}a_{3z} - a_{2z}a_{3y} & a_{3y}a_{1z} - a_{3z}a_{1y} & a_{1y}a_{2z} - a_{1z}a_{2y}\\ a_{2z}a_{3x} - a_{2x}a_{3z} & a_{3z}a_{1x} - a_{3x}a_{1z} & a_{1z}a_{2x} - a_{1x}a_{2z}\\ a_{2x}a_{3y} - a_{2y}a_{3x} & a_{3x}a_{1y} - a_{3y}a_{1x} & a_{1x}a_{2y} - a_{1y}a_{2x}\end{array}\right)$$

$$=\frac{(\begin{array}{ccc}\mathbf{a_2} \times \mathbf{a_3} & \mathbf{a_3} \times \mathbf{a_1} & \mathbf{a_1} \times \mathbf{a_2}\end{array})}{a_1\cdot(a_2\times a_3)}$$

基本逆格子ベクトルはこうなる。

$$\begin{eqnarray}2\pi A^{-1} \mathbf{e_1} &=&2\pi \frac{(\begin{array}{ccc}\mathbf{a_2} \times \mathbf{a_3} & \mathbf{a_3} \times \mathbf{a_1} & \mathbf{a_1} \times \mathbf{a_2}\end{array})}{a_1\cdot(a_2\times a_3)} \mathbf{e_1}\\ \\ &=&2\pi \frac{\mathbf{a_2} \times \mathbf{a_3}}{a_1\cdot(a_2\times a_3)}\\ \\ 2\pi A^{-1} \mathbf{e_2}&=&2\pi \frac{\mathbf{a_3} \times \mathbf{a_1}}{a_2\cdot(a_3\times a_1)}\\ \\ 2\pi A^{-1} \mathbf{e_3}&=&2\pi \frac{\mathbf{a_1} \times \mathbf{a_2}}{a_3\cdot(a_1\times a_2)} \end{eqnarray}$$

分母のベクトル三重積はどれも同じ値である。

これらはよく教科書に載っている基本逆格子ベクトルの式と一致する。

コメント