水晶発振回路の動作原理について
恥ずかしながら今まで真面目に勉強してこなかったので、水晶発振回路の動作原理を真面目に調べてみた。
よく使われるのはインバータを用いたこういうやつである。
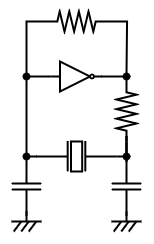
これの動作を説明できるようになりたい。
発振回路の原理
発振回路は主に弛張型発振回路と帰還型発振回路の2つに分類される。
水晶発振回路は帰還型発振回路に分類され、コルピッツ発振回路やハートレー発振回路、移相型発振回路などもこれにあてはまる。これらは正帰還の作用によって発振する。
負帰還を持つフィードバック回路の場合、最終的に出力値は入力値のあるゲイン倍に落ち着く。しかし正帰還を持つフィードバック回路の場合、その出力は回路的な限界に達するまで無限に増大し続ける。
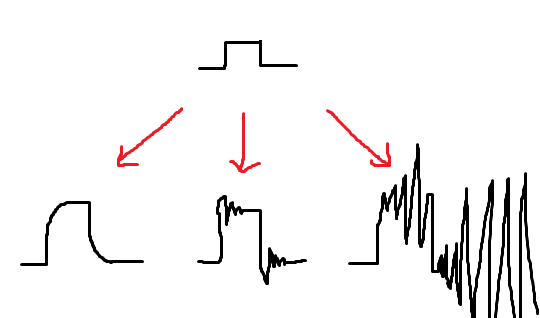
この働きによって、わずかな雑音などを種に発振が起きるのである。増幅回路やフィルタ回路であれば発振は大敵だが、発振回路はこれが目的となる。
上手く発振しない場合、発振の種として最初に少しパルスを入れるといった手法も使われる。
帰還回路の解析
フィードバック回路をブロック線図で表すと一般に以下のようになる。
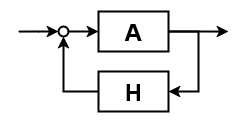
この回路全体の入出力間のゲインは$\frac{A}{1-AH}$と計算されるが、それが成り立つのは負帰還のときだけだ。正帰還であれば際限なく増大するので、そもそも「ある定数のゲイン値」という概念自体が成立しない。そこで負帰還か正帰還かを判別するため、ループを適当な位置で切り開き、一周のゲインを計算するということが行われる。これをオープンループゲインと呼ぶ。
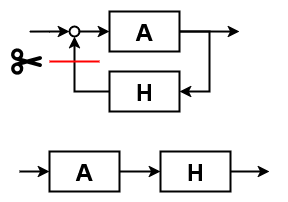
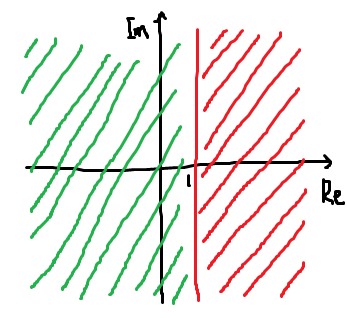
この$AH$の複素ゲイン実部が1以上なら正帰還だし、1未満なら負帰還となる。
余談:語義の混乱
先ほどは$AH$の値を「オープンループゲイン」と呼んだ。本記事では以降この呼び方で呼ぶ。
しかし一方で、上のブロック図で言う$A$を「オープンループ伝達関数(開ループ伝達関数)」、$AH$を「一巡伝達関数」と呼び分ける流儀もあるようだ。つまり「オープンループ」という単語には
- ループを切り開いた上で入出力の間を見る($=A$)
- ループを切り開いたときの一周を見る($=AH$)
の2通りの解釈があることになる。$H=1$の場合は一致するが、そうでない場合は話が変わってしまう。
この記事では「オープンループ」と言ったら$AH$のこと、つまり呼び分ける流儀における「一巡伝達関数」を指すものとする。
状態保持回路との比較
ところで、正帰還がかかった回路の用途には発振回路以外に、フリップフロップやヒステリシス回路といった状態保持回路もある。発振回路と状態保持回路はどう違うのだろうか。
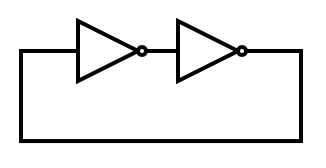
これら状態保持回路のオープンループは直流入力に対しても正のゲインを持つ。そのため+の飽和と-の飽和で2値の状態の保持が出来るが、発振回路はそうではない。発振回路は直流でのオープンループゲインを調べても正帰還は成立していない。
発振回路は直流に対してはゲインを持たない、もしくは負のゲインを持っており、特定の周波数でのみ正帰還が成立している。それによって発振という挙動になる訳だ。
単純な発振回路としてリングオシレータを例にとって考えてみよう。
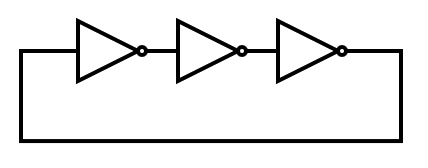
これは直流では当然大きな負のゲインを持っている。したがって愚直に考えれば負帰還回路ということになってしまう。しかし周波数が高くなってくると、伝播遅延の影響で位相が回ってくる。同じ$T$秒の遅延だとしても、角周波数$\omega$であれば$\omega T$ラジアンの位相回転に相当する。十分に周波数が高くなればもっと位相は回り、正の領域まで到達する。これによって発振回路として成立することが分かる。
バルクハウゼンの発振条件
発振が起きる必要条件を数式で説明したのがバルクハウゼンの発振条件というものである。 オープンループ伝達関数$AH$が以下の条件を満たす場合に系は発振する。
- $|AH|\geq 1$
- $\arg AH = 0^\circ$
ゲインが1以上で、位相が0度(360度)のときに発振する。この式を用いれば回路が発振するかどうか、またどの周波数で発振するかを定量的に議論することができる。
直感的解釈としては、まずゲインが1以上でないと正帰還がかからず減衰してしまい、そして位相がぴったり360度回っていないと信号が一周回ったときに合致しない、といったところか。
余談:180度を基準とする議論について
フィードバック回路について調べていると、「180度まで回ると発振してしまうので~」「180度までの位相余裕は~」といった形の議論も多々見かける。なぜ360度ではなく180度なのだろうか?
あれは何かというと、以下のようなブロック線図を前提とする場合にはオープンループゲインが$AH$ではなく$-AH$になるためだ。ゲインが-1倍されているので、$AH$の位相に追加でさらに180度回ることが前提になっているのである。
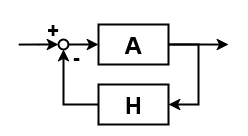
オープンループ一周分の位相としてはやはり360度回る必要があるということに変わりはない。
余談:発振条件の別表示
バルクハウゼンの発振条件のうち、2番目の位相条件を以下のように表記する場合もある。
- $\mathrm{Im}[AH]=0$
しかし、虚部が0でも実部が負の場合は負帰還になり、発振しないはずである。計算には便利だが気を付けたい。
余談:360度に達しない場合どうなるか
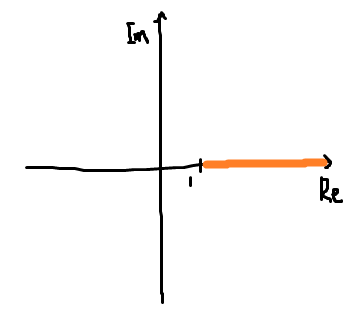
位相が0度(360度)でなくても正帰還さえあれば、つまりゲインの実部が正でさえあれば発振してくれそうな気がしてしまう。以下のように、ある周波数において$\mathrm{Re} [AH] > 1$だが位相はギリギリ360度に達しない場合はどういう挙動になるだろうか?
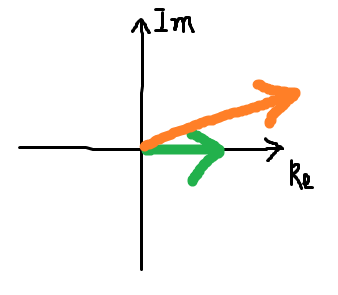
外部入力を0とすれば、この$AH$の値がそのまま次の回路入力になる。
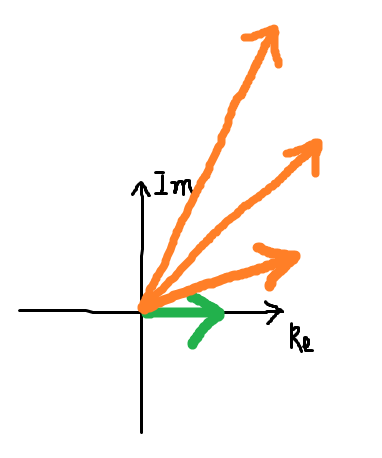
これが連鎖していくと、位相はどんどん回転していってしまい、一方向に留まらないことが分かる。つまり、その周波数で発振し続けることはない。
もう少し考えを進めてみよう。このフェーザ表示はある特定の周波数・位相の信号を基準として考えていたのだった。そのフェーザ図上で回転し続けるとしたら、それはどういうことだろうか?
それは別の周波数で発振しているということになる。100Hzを基準としたフェーザ図上で少しずつ位相が遅れて回転し、2Hzの速さで回転しているとしたら、それは98Hzの信号ということになる。少しずつ位相が進んで回転しているなら102Hzだ。ずっとそれが保たれているという場合、それは98Hz(あるいは102Hz)においてバルクハウゼンの発振条件が満たされているはずである。
バルクハウゼンの発振条件はあくまで「ある周波数において発振するかどうか」を判断する指標であり、別の周波数で発振しないということまで判断できるものではない。むしろバルクハウゼンの発振条件を満たす周波数において回路は発振するのである。
余談:位相の傾きについて
発振するかどうか自体を判断したい場合、オープンループ伝達関数のボード線図を使う方がよい。これの位相回転が360度に達していて、そこでゲインが0dBを超えているならそこで発振する。
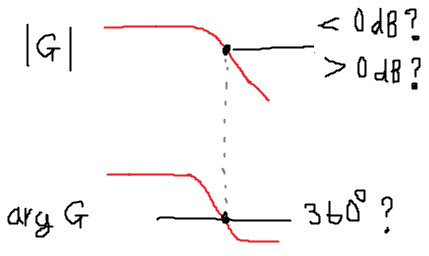
ところで、位相のグラフが360度のラインに触れるには2通りの場合があると考えられる。上(進み位相)から下(遅れ位相)に抜ける場合と下から上に抜ける場合だ。
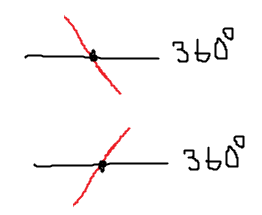
このうち、上から下に抜ける方は一般的だが下から上に抜ける方は一般的ではない。なぜか。
そもそも大抵の場合、位相のずれというのは根本的に遅延によるものなので、周波数が高くなるほど遅れ位相になる現象の方が圧倒的に一般的だという事情がある。こうした物理的な理由がまず1つ。
そしてもう1つ工学的な理由として、発振の安定性の問題がある。
上から下に抜ける場合、これはつまり周波数が小さければ進み位相になり(=周波数が上がり)、周波数が大きければ遅れ位相になる(=周波数が下がる)ので、周波数のわずかなずれが勝手に矯正される安定な発振点になることが分かる。
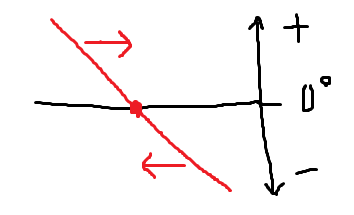
一方で下から上に抜ける場合、これは逆にわずかなずれが大きく拡大される不安定な発振点になってしまう。これでは発振回路として全く実用に耐えない。
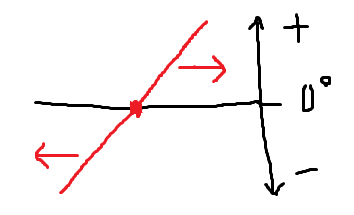
こうした理由から、位相が進み位相から遅れ位相になっていく方の点のみが発振に使われると考えられる。
水晶発振回路のオープンループ
水晶発振回路も、適当な場所で切り開いてオープンループゲインを調べることで仕組みを説明できるはずである。
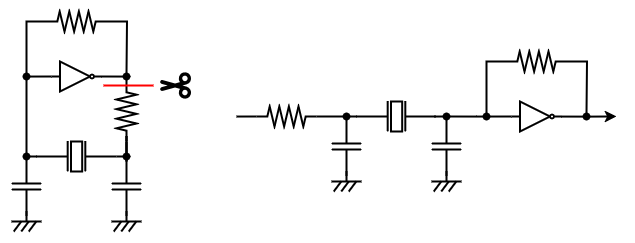
回路をブロックに分けて考えると
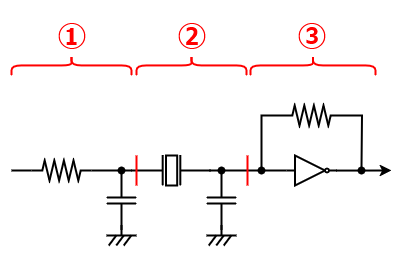
- RCローパスフィルタ
- 水晶振動子とCによるバンドパスフィルタ
- インバータによる反転増幅回路
の3つが繋がった形になる。
受動素子によるフィルタをちゃんと計算する場合、単純に分割して縦続接続として考えてしまうと問題があるのだが、大雑把な挙動を理解する上では便利である。
順番は前後するが、②→①→③の順で解説しよう。
水晶振動子によるバンドパスフィルタ
水晶は圧電(ピエゾ)素子の一種であり、電気信号を機械的圧力に変換したり、逆に機械的圧力を電気信号に変換したりすることができる。機械的圧力は素子を変形・振動させる。
音叉と同様の原理によって、機械的振動は特定の周波数だけ残りやすい。これを利用したのが水晶振動子である。実際には内部で機械的に素子が振動しているのだが、電気的には非常に性能の良いバンドパスフィルタに見える訳だ。
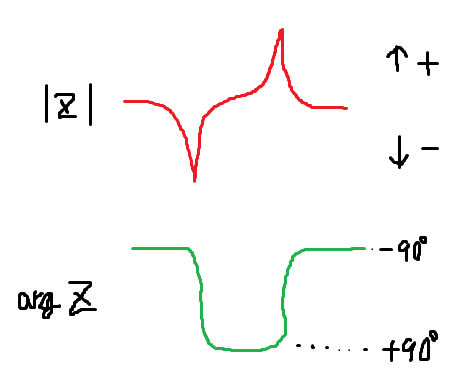
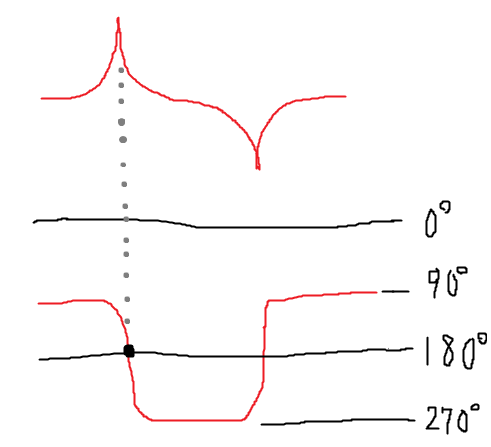
水晶振動子は以下のような周波数特性を持つ。共振周波数(直列共振周波数)でインピーダンスが極小をとり、反共振周波数(並列共振周波数)でインピーダンスが極大をとる。
またインピーダンス角としては、共振周波数以下ではほぼ-90度(=コンデンサ的)であり、共振周波数~反共振周波数の間では+90度(=インダクタ的)になる。
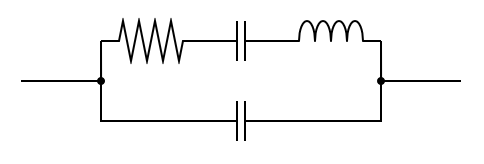
水晶振動子の等価回路は以下のものがよく使われる。RLC直列の部分が共振部分を表している。ただしこの形の等価回路では不十分な場合もある。(後述)
水晶振動子とキャパシタによるフィルタ回路は以下のような周波数特性を持つ。
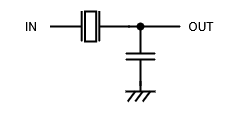
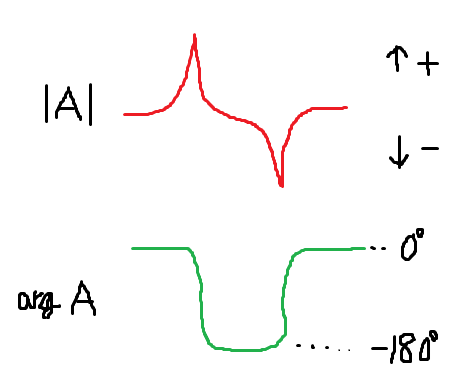
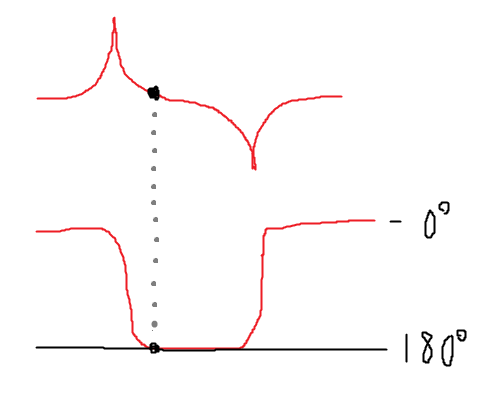
共振周波数で水晶のインピーダンスが極小となり、ゲインは極大を取る。また位相としては、DC~共振周波数にかけては位相の回転を起こさず、共振周波数で180度位相回転し、反共振周波数で再び元に戻る。
この共振周波数でゲインが大きくなり、また位相が180度回転する特性を発振に使う。
余談:オーバートーン
実は、水晶は共振周波数の3倍、5倍、7倍...といった奇数倍の周波数にも共振点を持つ。これをオーバートーンという。グラフで表すと以下のようなイメージである。
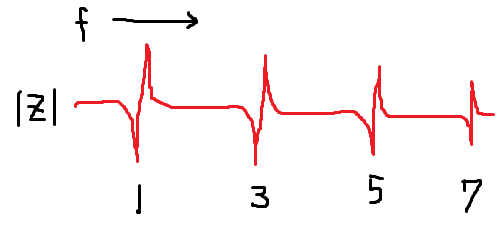
この理由は学校の理科の時間で習ったような共振現象を考えると分かりやすい。片側固定端の振動は基本振動の奇数分の1の波長=奇数倍の周波数に共振点を持つ。
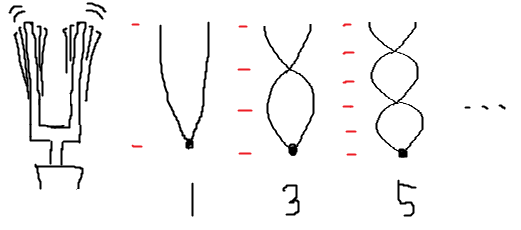
回路特性の調整次第では、こうした3倍、5倍、7倍などのオーバートーン周波数による発振をすることもある。意図せず起こることもあるし、意図的にオーバートーン発振をさせる場合もある。
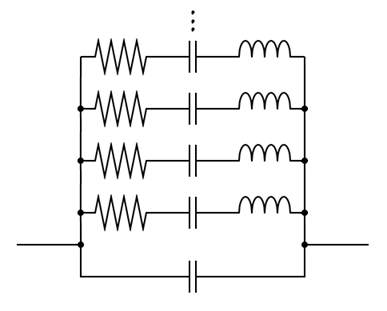
ところで、先ほど挙げたRLC+Cによる等価回路の場合は1か所しか共振点がなく、当然オーバートーン発振のシミュレーションは出来ない。この問題を解決したい場合、以下のようなより正確な等価回路モデルを用いる必要がある。
RCフィルタ
これはおそらくいくつかの役割がある。
- インバータから水晶へ過大な電流が流れるのを抵抗によって抑える(特にインピーダンス極小の共振周波数において)
- ローパスフィルタとして高周波のゲインを抑え、オーバートーンによる発振を抑える
- 位相回転(位相シフト)によって180度の位相回転を安定させる
1番目と2番目については分かりやすいと思う。このRCフィルタが無かったら水晶に大量の電流が流れ、またオーバートーン特性によって意図せず高い周波数で発振してしまうリスクがある。
3番目について詳しく説明する。
先述のように、発振するためにはオープンループの位相が360度回る必要がある。インバータが180度分回すので、後の受動素子部分で180度回さなければならない。水晶によるフィルタ部分は共振周波数においてちょうど180度位相を回転させるが、実際には多少なまった特性になることも含めると共振点からずれてしまい、全く余裕のない設計になってしまう。
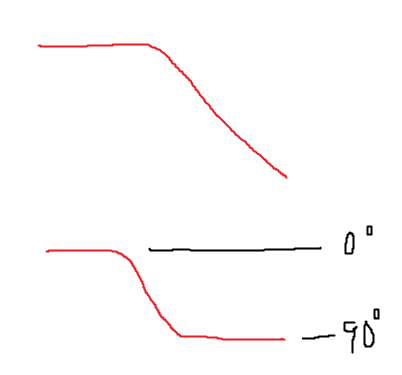
そこでRCフィルタを入れる。RCフィルタは一定の周波数以上で0~90度の位相回転を起こす。
これを入れると90度の位相シフト分である程度余裕を持った設計になるのではないだろうか。0度~180度だったのがおおよそ90度~270度になってくれる。180度のラインは共振周波数に余裕を持って一致する。
なお実際には、共振点までで完全に90度シフトするような設計は必ずしもされない。なので共振周波数周辺での位相のグラフは90度~270度とは限らず、60度~240度とか80度~260度のような形になると思われる。いずれにしろ位相シフトのおかげで余裕を持った設計になる。
この位相に関する点を明確に書いている資料が見当たらなかったのだが、恐らくかなり重要な点だと思う。
RCフィルタの抵抗が小さすぎると位相シフトが起こる極は高周波側にずれてしまい、この恩恵をあまり得られなくなってしまう。水晶への電流も大きくなる。一方で、抵抗が大きすぎると今度は回路全体のゲインが減ってしまい、発振しにくくなる。この点で丁度良い抵抗値を選ぶ必要がある。
- 例: C=22pF、周波数f=8MHz → $R>1/2\pi f C \approx 0.9[k\Omega]$
- 例: C=22pF、周波数f=32768Hz → $R>1/2\pi f C \approx 220[k\Omega]$
インバータ
このインバータはよく「アンバッファタイプでなければならない」といった注意がされる。それはなぜだろうか。アンバッファタイプの方が高速だからだとかそういうことではない。
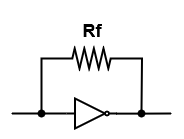
回路を見ると目を引くのが$R_F$というフィードバック抵抗だ。実は、このインバータはフィードバック抵抗と一緒に反転増幅回路として機能している。それゆえにアナログな線形性が重要なのだと思われる。
等価なオペアンプ回路の形に直すとこうだ。
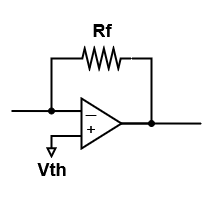
こうすると入力インピーダンス$R_F$の反転増幅回路であることが分かりやすい。
回路全体の挙動
シミュレーションしてみると、回路全体のゲインと位相は以下のようになる。回路定数はCQ connectの記事を参考にした。(リンク)
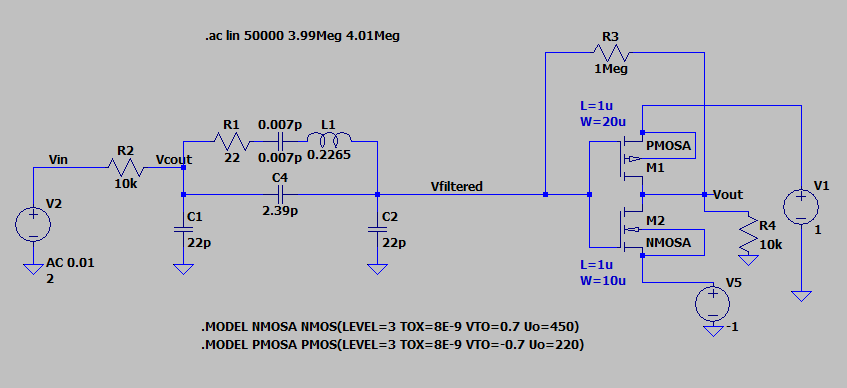
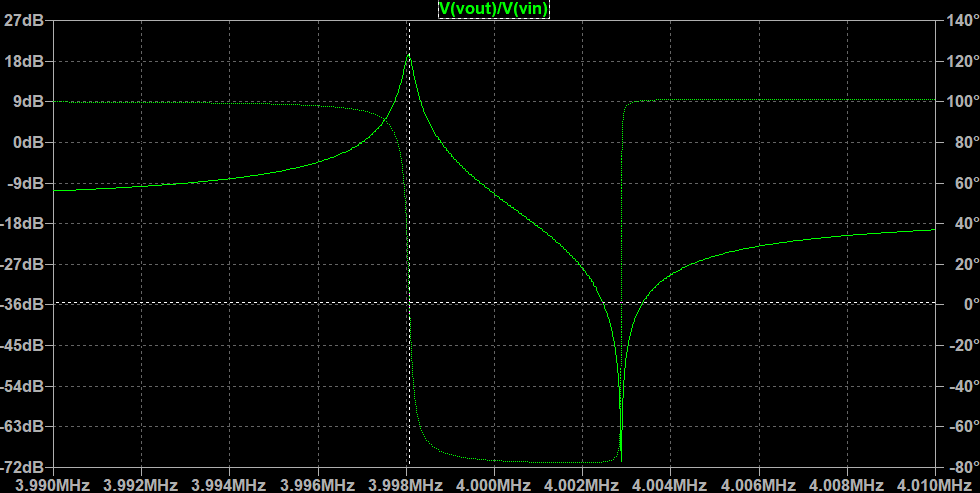
共振周波数において位相が0度を横切っており、またゲインが0dB(=1倍)を超えているのでここで発振することが分かる。なお反共振周波数でも位相が0度になっているが、こちらではゲインが0dBを下回っているので発振しない。また仮にゲインが1を超えていたとしても、位相の微分が正になっているため発振は非常に不安定になる。
その他、混乱しやすそうな点
振幅の収束について
水晶は立ち上がって動作が安定するのに結構時間がかかる。シミュレーションしてみて、発振するが振幅が妙に小さいという場合は、単純にまだ振幅が立ち上がっていないというだけかもしれない。1msのシミュレーションでは立ち上がらなくても10msのシミュレーションでは十分な振幅に育っている、10msのシミュレーションでは発振してないように見えても100msの間には立ち上がっているというケースがある。
インバータの増幅能力などによってこの長さはかなり変わる。ここについてはまだあまり調べが付いていないので、詳しく分かったら改めて記事にしたい。
ゲインはいかに最終的に1に落ち着くか
ゲインが1以上であれば発振する。が、もし本当にずっとゲインが1を超えていれば、際限なく指数関数的に振幅が大きくなるはずである。実際にはあるところでゲインが1になり、定常発振状態に落ち着く。
増幅回路には飽和があるので当然の結果ではあるが、理論解析としてはこの現象をどのように解釈すべきだろうか。
最も一般的な手は、増幅回路のゲインを振幅に依存して変化する関数と考える方法と思われる。振幅が大きくなるにつれ、回路は飽和に近づきゲインは小さくなり、あるところでゲインは1になる。
インバータ入力側の信号について
インバータ出力は飽和のために矩形波に近い形になるのに対し、入力側はほぼ正弦波に近い波形になる。これは水晶振動子が極めてQ値の高いバンドパスフィルタとして機能していることを考えれば当然のことだろう。特定の周波数成分しか通さないのだから。
それから安定動作中の水晶発振回路においてインバータ入力側の振幅を見て見ると、出力側より電圧の振幅が大きかったりする。なんなら電源電圧を超えていたりする。これはどういうことだろう。
既に説明した通り、水晶は非常にQ値の高いBPFとして動作する。受動素子なので電源電圧で飽和することもない。従って矩形波を入力したらほぼその基本波が取り出されると考えてよい。
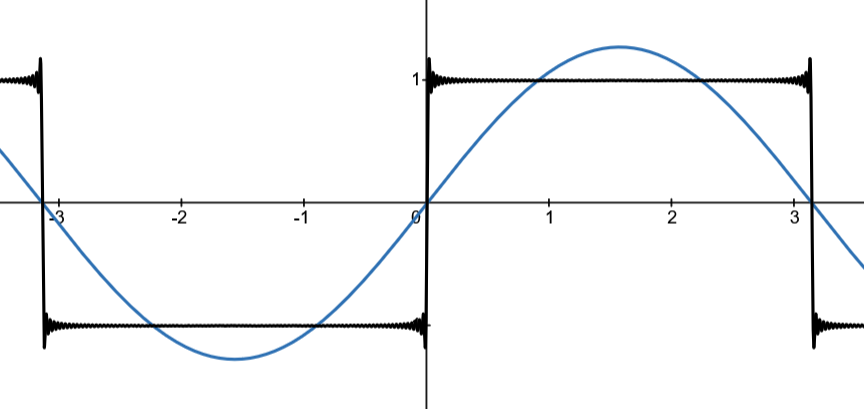
振幅1の矩形波のフーリエ級数展開は以下の式で表される。
$$y=\frac{4}{\pi}\left(\sin(x) + \frac{1}{3}\sin(3x)+ \frac{1}{5}\sin(5x) + \cdots \right)$$
基本波は$\frac{4}{\pi}\sin(x)$だ。従って矩形波を入力した場合はその $4/\pi \approx 1.3$ 倍程度の振幅が発生しうるということになる。
例えば5V電源で動作させて電源電圧/2を中心に発振したとすると、
- 最小値: $2.5[V] - 1.3 \times 2.5[V] = -0.75[V]$
- 最大値: $2.5[V] + 1.3 \times 2.5[V] = +5.75[V]$
瞬時値としてこの程度の電圧が発生しうる。
実際には電源電圧より狭い範囲で飽和するのでこれよりは小さくなるとは思うが、デリケートな部品を使う場合は素子の耐圧をある程度気にするべきかもしれない。
負性抵抗法について
発振回路の設計方法としてしばしば「負性抵抗」を用いた説明がなされる。これは、本来LC共振によって発振するものがR成分によって減衰してしまうところを、負の抵抗によって打ち消すことで発振させるのだ…と等価的にみなすやり方である。
いまひとつどういう旨味があってこのような考え方をするのか分かっていないので、理解出来たらこれも別途記事にしたい。